Working Paper Series no. 688: Estimating Non-Linear DSGEs with the Approximate Bayesian Computation: an application to the Zero Lower Bound
Estimation of non-linear DSGE models is still very limited due to high computational costs and identification issues arising from the non-linear solution of the models. Besides, the use of small sample amplifies those issues. Valerio Scalone advocates for the use of Approximate Bayesian Computation (ABC), a set of Bayesian techniques based on moments matching. First, through Monte Carlo exercises, he assesses the small sample performance of ABC estimators and runs a comparison with the Limited Information Method (Kim, 2002), the state-of-the-art Bayesian method of moments used in DSGE literature. He finds that ABC has a better small sample performance, due to the more efficient way through which the information provided by the moments is used to update the prior distribution. Second, ABC is tested on the estimation of a new-Keynesian model with a zero lower bound, a real life application where the occasionally binding constraint complicates the use of traditional method of moments.
Despite the growing importance of non-linear DSGE models, their estimation is still very limited mainly due to the high computational burden associated to the non-linear estimation techniques. Beside, some identification issues can arise due to non-regularities deriving from the non-linear solution.
Are there estimation methods which overcome those issues and make non-linear DSGE estimation easier to apply? The Bayesian versions of the methods of moments can provide a useful response in this sense. In particular, this paper advocates for the use of Approximate Bayesian Computation, a set of techniques developed in epidemiology and population genetics (Pritchard et al. [2000]).
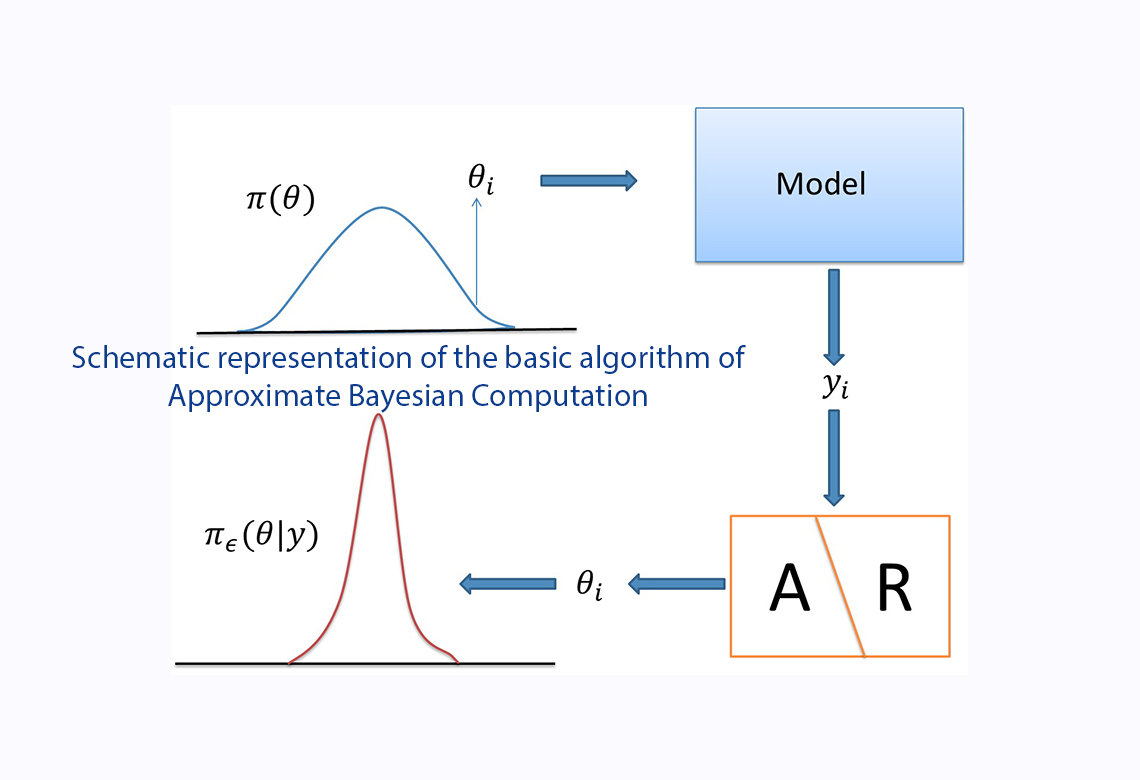
ABC is a set of Bayesian methods through which the prior distribution of the structural parameters of the model is updated by the information provided by the moments (i.e. variances, covariances, etc.). In a first step, a large number of vectors of parameters is drawn from the prior distribution. In a second step, for each vector o parameter, the model is simulated. For each simulation, the distance between the vector of simulated moments and the vector of the observed moments is computed. In a third step, a selection step is made for each simulation: simulations are accepted only if the Euclidean distance is smaller than a fixed threshold, otherwise they are rejected. Finally, the parameters associated to the accepted simulations provide an approximation to the posterior distribution.
Through Monte Carlo exercises, I show that ABC has a better small sample performance compared to the state-of-the-art Bayesian method of moments used in DSGE estimation, the Bayesian Limited Information (Kim [2002], Christiano et al. [2015]). This result hinges on the way through which the distribution of the moments is obtained and used to update the prior distribution.
Furthermore, I estimate a New-Keynesian DSGE model with an occasionally binding ZLB by using simple ABC-rejection. I estimate the model on US data by using ABC and I find three results. First, including the period of the ZLB in the sample is crucial to correctly estimate the probability of hitting the Zero Lower bound. Second, the use of conditional moments in the estimation (i.e. moments conditional on the state of the economy) can ease the identification issues generated by the presence of the Zero Lower Bound. Third, estimation helps the model to replicate some of the main features observed before and after the Great Recession and to ease the over-reaction of macroeconomic variables predicted by the DSGE with ZLB, as highlighted by Fernandez-Villaverde [2015].
Download the PDF version of this document

- Published on 08/10/2018
- 50 pages
- EN
- PDF (1001.84 KB)
Updated on: 08/10/2018 16:47