Working Paper Series no. 670: The Optimal Inflation Target and the Natural Rate of Interest

The inflation aim central banks commit to achieve is a key dimension of modern monetary policy strategy. Among the reasons of having a strictly positive inflation are the costs induced by the zero lower bound (ZLB) on interest rates. The ZLB hampers the ability of monetary policy to stabilize the economy, bringing about more frequent (and potentially protracted) episodes of recessions and below-target inflation. A positive inflation target can be beneficial as it increases the steady-state level of nominal interest rates and therefore limits the probability of ZLB episodes.

Recent research, often associated with the notion of “secular stagnation”, emphasizes that real interest rates may have structurally declined over the past decade. This is important for monetary policy:  For a given average inflation, a lower steady-state real rate would cause the nominal interest rate to hit its ZLB more frequently. In face of that risk, and in order to counteract it, several prominent economists have forcefully argued in favor of raising the inflation target. While the proposal is quite intuitive, the answer to the practical question of by how much should the target be increased is not obvious. Indeed the benefits of limiting the probability of hitting the ZLB, which is an infrequent event, have to be compared with the higher distortion costs involved by a permanent increase in the inflation target.

The present paper addresses this question by assessing how the trade-off between the cost of inflation and the cost of the ZLB is affected by such potential structural drop in the real rate of interest.  More precisely we use a structural, empirically estimated, macroeconomic model to characterize how the optimal inflation target (π*) is related to the steady-state real interest rate (r*) and whether the source of variations in such steady-state real interest rate matters for this relation.

Our results are obtained from extensive simulations of a New Keynesian DSGE model estimated for both the US and the euro area. The framework features: (i) price stickiness and imperfect indexation of prices to non-zero trend inflation, (ii) wage stickiness and imperfect indexation of wages to both inflation and technical progress, and (iii) a ZLB constraint on the nominal interest rate. The first two features imply the presence of potentially substantial costs associated with non-zero wage or price inflation. The third feature warrants a strictly positive inflation rate, in order to mitigate the incidence and adverse effects of the ZLB. To our knowledge, these three features have not been jointly taken into account in previous analyses of optimal inflation.

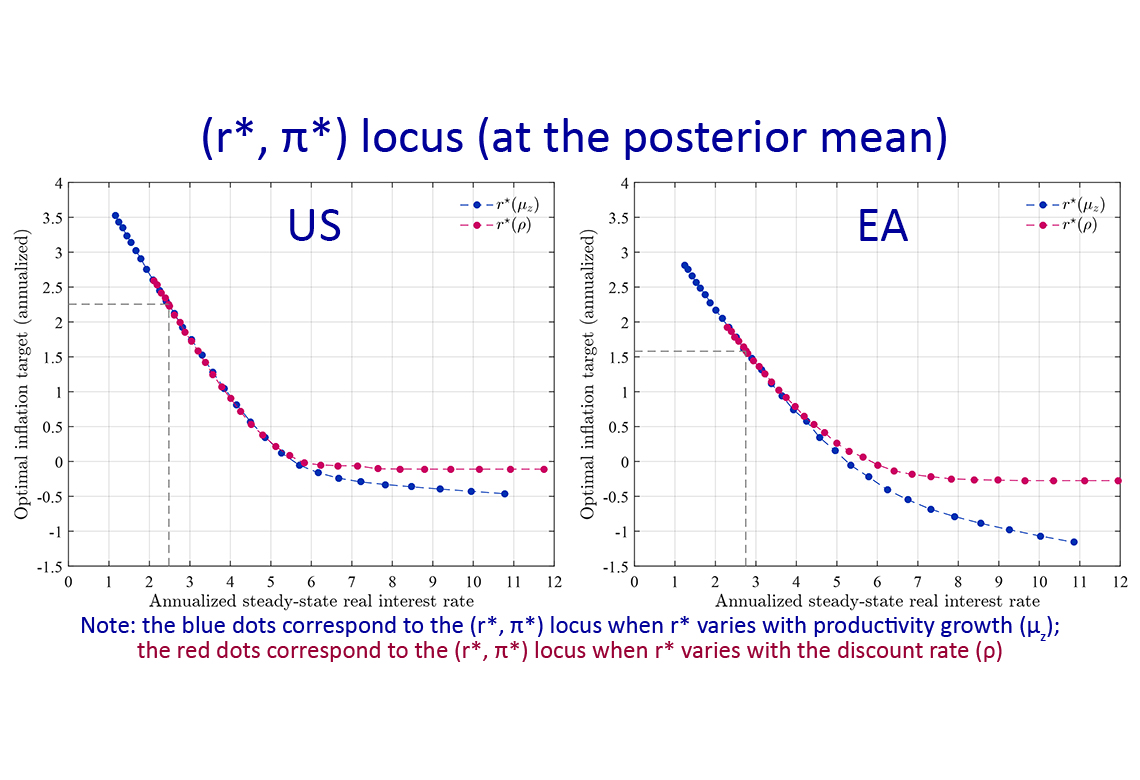
Figure above illustrates our main findings which can be summarized as follows: (i) The relation between r*and π*is downward sloping, but not necessarily one-for-one; (ii) in the vicinity of the pre-crisis values for r*, the slope of the (r*, π*) locus is close to -0.9; that is a 100 basis points decline in steady state real interest rate warrants an increase by 90 basis points of the inflation target; and (iii) for a plausible range of r* values the relation is largely robust to the underlying source of variation in r*.

As we perform a full-blown Bayesian estimation of the model on both US and euro area data, we can derive an optimal inflation target taking into account the parameter uncertainty facing the policy maker. When that parameter uncertainty - including uncertainty with regard to the determinants of the steady-state real interest rate - is accounted for, values of optimal inflation targets are found to be larger: 2.40% instead of 2% for the US and 2.20% instead of 1.5% for the euro area. However, simulations illustrate that the optimal inflation target still rises by about 90 basis points in response to a downward shift of the whole distribution in r*of 100 basis points.

That main result is robust to several alternative assumptions described in the papers.