Working Paper Series no. 830: Risk-to-Buffer: Setting Cyclical and Structural Capital Buffers through Banks Stress Tests
In this work we present the Risk-to-Buffer: a new framework to jointly calibrate cyclical and structural capital buffers, based on the integration of a non-linear macroeconomic model with a Stress test model. The macroeconomic model generates scenarios whose severity depends on the level of cyclical risk. Risk-related scenarios feed into a banks' Stress test model. Banks' capital losses deriving from the reference-risk scenario are used to calibrate the structural buffer. Additional losses associated to the current-risk scenario are used to calibrate the cyclical buffer.
Since the global financial crisis, prudential authorities have substantially reformed banks capital regulation framework. A new set of rules, labelled Basel III, entered into force to strengthen banks resilience in case of materialization of different types of risks. With respect to previous regulation, one of the novelties of Basel III consisted in introducing a distinction between: i) buffers that evolve with the financial cycle and ensure banks resilience against risks related to the evolution of financial conditions (cyclical buffers), ii) buffers which remain constant through the cycle and cover risks related to the structure of the banking system (structural buffers).
In practice, cyclical and structural buffers are often calibrated through Banks Stress test models. These models assess banks resilience through a set of econometric and accounting equations, projecting the evolution of bank capital and capital ratios (e.g. CET1 ratios) with respect to negative macroeconomic scenarios (so-called adverse scenarios). Based on banks' projected losses, authorities set capital requirements so that, should the adverse scenario materialise, banks would have enough capital to absorb those losses and remain resilient.
A formal framework to map projected capital losses into cyclical and structural buffers is still missing. Moreover, when cyclical and structural buffers are calibrated using different parallel Stress test exercises based on similar scenarios, different buffers might end up covering the same type of vulnerability, resulting in a double counting of risk in capital requirements.
In this paper, we propose a new conceptual framework, the Risk-to-Buffer, to jointly calibrate cyclical and structural buffers through the use of Stress tests.
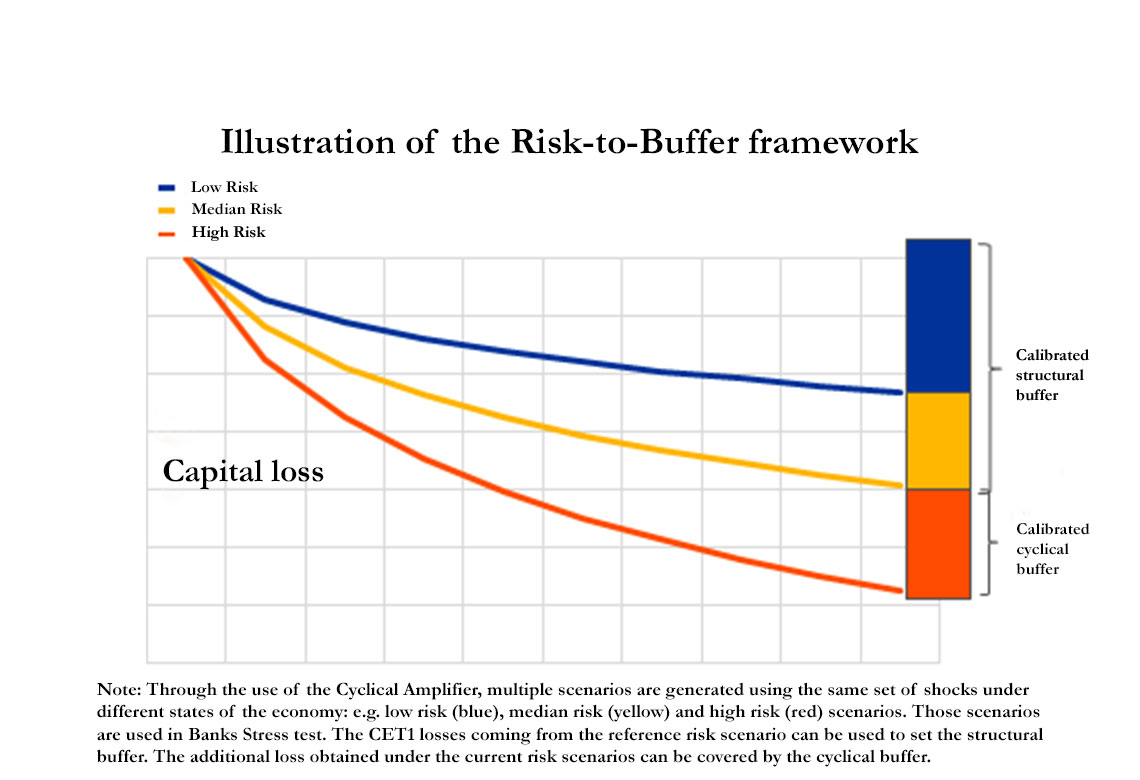
First, we use a non-linear macroeconomic model -which we call the Cyclical Amplifier- to generate adverse scenarios whose severity depends on the risk level, so to obtain a "reference"-risk scenario and a cyclical risk-scenario. In order to show how the Cyclical Amplifier works, we use it in an application on the Euro Area. We generate multiple adverse scenarios in which a fixed set of shocks hits the economy under different risk levels. Typically, a first scenario is produced at a reference risk level (e.g. historical median) to capture dynamics under a reference risk environment, and a second scenario is produced at the current risk level to capture the amplification role played by the current cyclical risk.
In a second step, the different scenarios are used as inputs in a stylised Stress test model to obtain corresponding CET1 ratio projections. Higher risk scenarios are associated with larger capital losses: under high risk the aggregate reduction of CET1 for European banks will be more than doubled with respect to the case of low risk, whereas under medium risk, the CET1 ratio depletion will be in between.
Following the Risk-to-Buffer approach, we set the structural buffer based on the losses obtained under the reference-risk scenario whereas the cyclical buffer is set based on the extra losses projected under the current-risk scenario. As such, this latter will evolve with the level of cyclical risk. Should the current risk level be lower than the reference risk (e.g. the one used to calibrate the structural buffer), the cyclical buffer would be set at zero. In this way, the sum of both buffers would not fall below the structural buffer, which acts as backstop on capital requirements.
In this way, first, structural and cyclical buffers cover different expected losses, tackling the risk of overlap. Second, the level of cyclical buffer is mechanically linked to the evolution of cyclical risk.
In an alternative calibration strategy, structural buffer would be equal to the loss obtained when the risk is at its historical minimum. This alternative calibration would imply a a positive cyclical buffer when risk is at its median, implying a positive "neutral level" for the cyclical buffer. The second calibration approach increases the relative importance of cyclical buffers, providing releasable buffers as soon as the current risk is higher than the historical minimum.
According to the calibration approach, the amplification of losses explained by the cyclical risk could cover form half to two thirds of the total CET1 depletion. A possible policy implication of this result goes in the direction to increase the space allocated to the cyclical buffer with respect to the current regulation.
Finally, our Risk-to-Buffer framework can be used to shed light on the interconnection between borrowers' based measures (e.g. prudential policy directly affecting indebtedness) and capital buffers.
Download the PDF version of this document

- Published on 09/08/2021
- 43 pages
- FR
- PDF (2.24 MB)
Updated on: 09/08/2021 16:28