Working Paper Series no. 920: Stochastic Simulation of the FR-BDF Model and an Assessment of Uncertainty around Conditional Forecasts
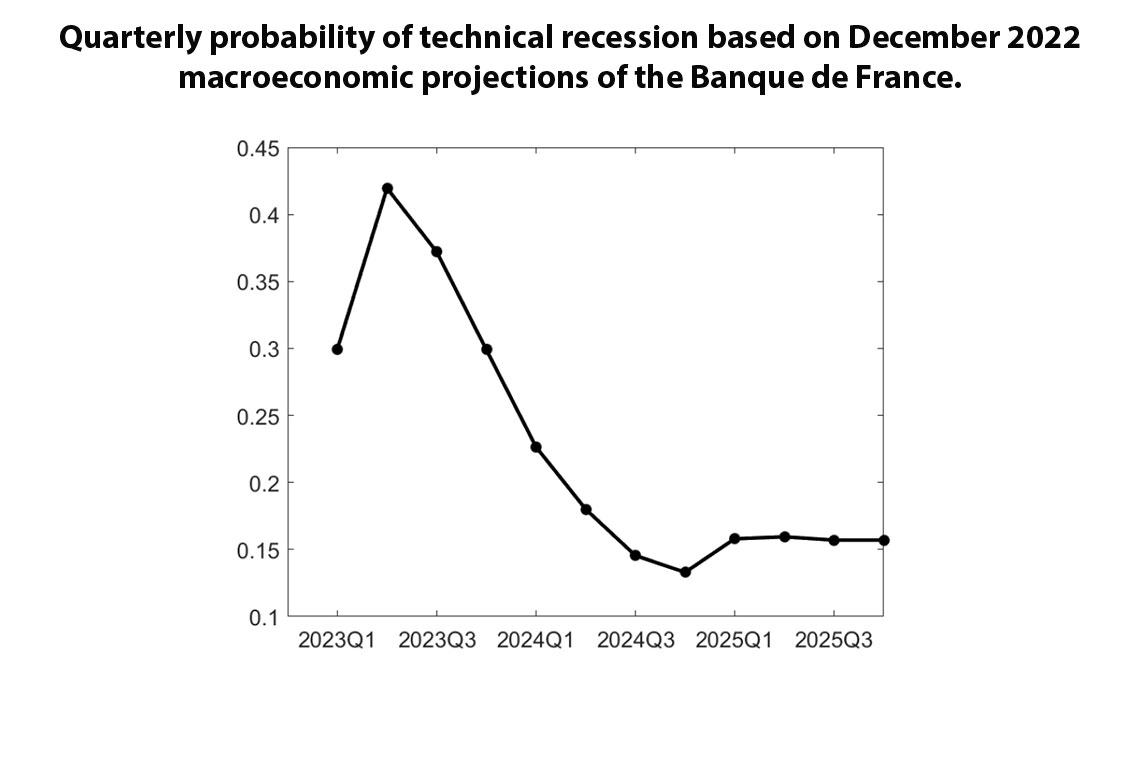
This paper presents a framework to introduce uncertainty into the FR-BDF model, used for macroeconomic projections and policy analysis at the Banque de France. Belonging to the semi-structural class of large-scale macroeconomic models, it is only fair to assume that FR-BDF may suffer from various types of misspecification. We do not seek to correct the latter, but instead we study its systematic nature using unobserved component models for the residuals of FR-BDF. Stochastic simulations based on random draws of innovations of these models allow us to work with applications that describe probabilities of events and risk in general. Applying this framework to the December 2022 forecast exercise of Banque de France, based on the available information at that time, the highest probability of observing a technical recession occurs in 2023Q2 and reaches 42%.
This paper focuses on developing a framework for the stochastic simulation of the FR-BDF model, which is used for medium-term economic forecasting and policy analysis. By incorporating randomness into the model, various new applications become possible, such as constructing confidence bands and fancharts around point forecasts, as well as analyzing probabilities of events and overall risk.
There are different ways to implement a stochastic framework, but the key requirement is the ability to generate random numbers that can be used as innovations in the model equations. One simple approach is bootstrapping, where random numbers are drawn from the unconditional distribution of historical residuals obtained from estimating the model. This method is easy to implement and ensures that the generated innovations align with the properties of the model and the available data.
However, bootstrapping has a limitation. It ignores potential intertemporal dependence within the residuals, which should also be present in the random innovations applied to the model. The FR-BDF model, like many others in its class, is susceptible to suffer from such issues because of possible misspecifications, such as omitted variables or incorrect functional forms. This potential misspecification can lead to residuals that have predictable patterns due to unmodeled features of the data.
To address this challenge, we propose a solution that leverages the systematic nature of the misspecification. We assume that this systematic behavior can be captured using an Unobserved Components Model (UCM), which splits the residuals into two components: one persistent and one transitory. These components are both unobservable but follow a Gaussian distribution. The task is to estimate the parameters of the UCM to distinguish between the two components.
Similar frameworks have been implemented by other central banks with semi-structural models. The ECB, for example, uses a similar approach on the residuals of the ECB-BASE model, while the Federal Reserve's FRB/US model employs different sampling frameworks, including bootstrapping and state-contingent methods.
The estimation results for the FR-BDF model indicate some degree of misspecification. The UCM parameter estimates reveal significant persistence in the residuals from one period to the next, although the degree of persistence varies across equations. Some equations have economically insignificant persistence, while others, such as those related to exchange rates, public sector employment, and non-energy imports, exhibit larger persistence.
A practical application of the framework involves analyzing the uncertainty bands based on the December 2022 macroeconomic projections of the Banque de France. The simulations are designed to retain all conditioning information by inverting the full forecast and obtaining baseline paths for exogenous stochastic shocks. This allows for a close replication of the forecast, with the mean of the stochastic simulations matching the forecast.
The usefulness of the proposed framework is demonstrated by estimating, on a quarterly basis, the probability of a technical recession, defined as negative GDP growth in two consecutive quarters. Based on the available information at that time, we calculate the probability of a technical recession in France from 2023Q1 to 2025Q4. We find a peak of 42% in 2023Q2 and a decrease to 16% by the end of the period, see Figure 1. The probability increases notably in 2025 due to convergence to the trend. Note that, based on available GDP data, technical recession did not realize in early 2023.
Download the PDF version of this document

- Published on 08/10/2023
- 28 pages
- EN
- PDF (2.04 MB)
Updated on: 08/10/2023 09:59