Working Paper Series no. 713: Bayesian MIDAS penalized regressions: estimation, selection, and prediction

The outstanding increase in the availability of economic data has led econometricians to the development of new regression techniques based on Machine Learning algorithms, such as the family of penalized regressions. This consists in regressions with a modified objective function, such that coefficients estimated close to zero are shrunk to exactly zero, leading to simultaneous selection and estimation of coefficients associated to relevant variables only. While some of these techniques have been successfully applied to multivariate and usually highly parameterized macroeconomic models, such as VARs, only a few contributions in the literature have paid attention to mixed-frequency (MIDAS) regressions. In the classic MIDAS framework, the researcher can regress high-frequency variables (e.g. monthly variables such as surveys) directly on low-frequency variables (e.g. quarterly variables such as GDP) by matching the sampling frequency through specific aggregating (weighting) functions. The inclusion of many high-frequency variables into MIDAS regressions may nevertheless lead to overparameterized models, with poor predictive performance. This happens because the MIDAS regression approach can efficiently address the dimensionality issue arising from the number of high-frequency lags in the model, but not that arising from the number of high-frequency variables. Hence, recent literature has focused on MIDAS penalized regressions, based mainly on the so-called Lasso and Elastic-Net penalizations.

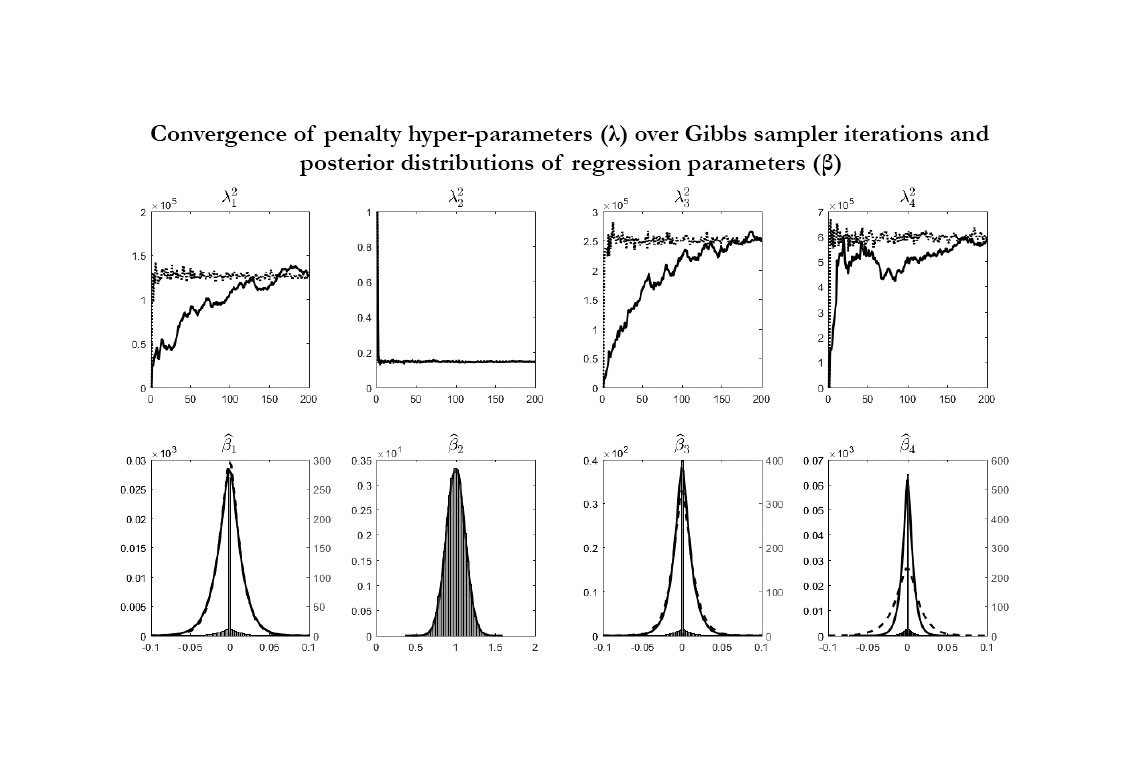
In the present paper, we propose a similar approach, but we depart from the existing literature on several points. First, we consider MIDAS regressions resorting to Almon lag polynomial weighting schemes, which depend only on a bunch of functional parameters governing the shape of the weighting function and keep linearity in the regression model. Second, we consider a Group Lasso penalty, which operates on distinct groups of regressors, and we set as many groups as the number of high-frequency predictors, allowing each group to include the entire Almon lag polynomial of each predictor. This grouping structure is motivated by the fact that if one high-frequency predictor is irrelevant, it should be expected that zero-coefficients occur in all the parameters of its lag polynomial. Third, we implement Bayesian techniques for the estimation of our penalized MIDAS regressions. The Bayesian approach offers two attractive features in our framework. The first one is the inclusion of spike-and-slab priors that, combined with the penalized likelihood approach, aim at improving the selection ability of the model by adding a probabilistic recovery layer to the hierarchy. The second one is the estimation of the penalty hyper-parameters through an automatic and data-driven approach that does not resort to extremely time consuming pilot runs. In this paper we consider an algorithm based on stochastic approximations, which consists in approximating the steps necessary to estimate the hyper-parameters in such a way that simple analytic solutions can be used. It turns out that penalty hyper-parameters can be automatically tuned with a small computational effort compared to existing and very popular alternative algorithms. We show through simple numerical experiments (see Figure below) that the suggested procedure works well in our framework: penalty hyper-parameters (λ) converge fairly quickly to their optimal values (first panel), such that the estimated coefficients (β) for irrelevant predictors are correctly centered at zero with small variance (second panel). Most importantly, the results points to substantial computational gains compared to alternative algorithms that we evaluate by a factor of 1 over 15.

We use our MIDAS models in an empirical forecasting application to U.S. GDP growth. We consider 42 real and financial indicators, sampled at monthly, weekly, and daily frequencies. We show that our models can provide superior point and density forecasts at short-term horizons (nowcasting and 1-quarter-ahead) compared to simple as well sophisticated competing models. Further, the results suggest that high-frequency financial variables may have some, although limited, short-term predictive content for the GDP.