Document de travail n°713 : Régressions pénalisées MIDAS bayésiennes : estimation, sélection et prévision

L'accroissement remarquable du volume de données disponibles pour l’analyse macroéconomique a conduit les économètres à développer de nouvelles techniques de régression basées sur des algorithmes d'apprentissage statistique, comme la famille des régressions pénalisées. Il s'agit de régressions avec une fonction objective modifiée, de telle sorte que les coefficients estimés proches de zéro sont ramenés exactement à zéro, ce qui conduit à la sélection et à l'estimation simultanées des coefficients associés aux seules variables pertinentes. Bien que certaines de ces techniques aient été appliquées avec succès à des modèles macroéconomiques multivariés et habituellement hautement paramétrés, comme les VAR, seules quelques contributions dans la littérature ont porté sur les régressions à fréquences mixtes (MIDAS). Dans le cadre classique du MIDAS, le chercheur peut régresser les variables de haute fréquence (p. ex. les variables mensuelles comme les enquêtes) directement sur les variables de basse fréquence (p. ex. les variables trimestrielles comme le PIB) à travers un appariement des fréquences d'échantillonnage obtenu via des fonctions d'agrégation (pondération) spécifiques. L'inclusion de nombreuses variables à haute fréquence dans les régressions MIDAS peut néanmoins conduire à des modèles surparamétrés, affichant des mauvaises performances prédictives. Cela s'explique par le fait que l'approche de régression MIDAS peut résoudre efficacement le problème de dimensionnalité découlant du nombre de retards à haute fréquence dans le modèle, mais pas celui découlant du nombre même de variables à haute fréquence. Ainsi, la littérature récente s'est concentrée sur les régressions pénalisées MIDAS, basées principalement sur les pénalités dites de Lasso et d’Elastic-Net.

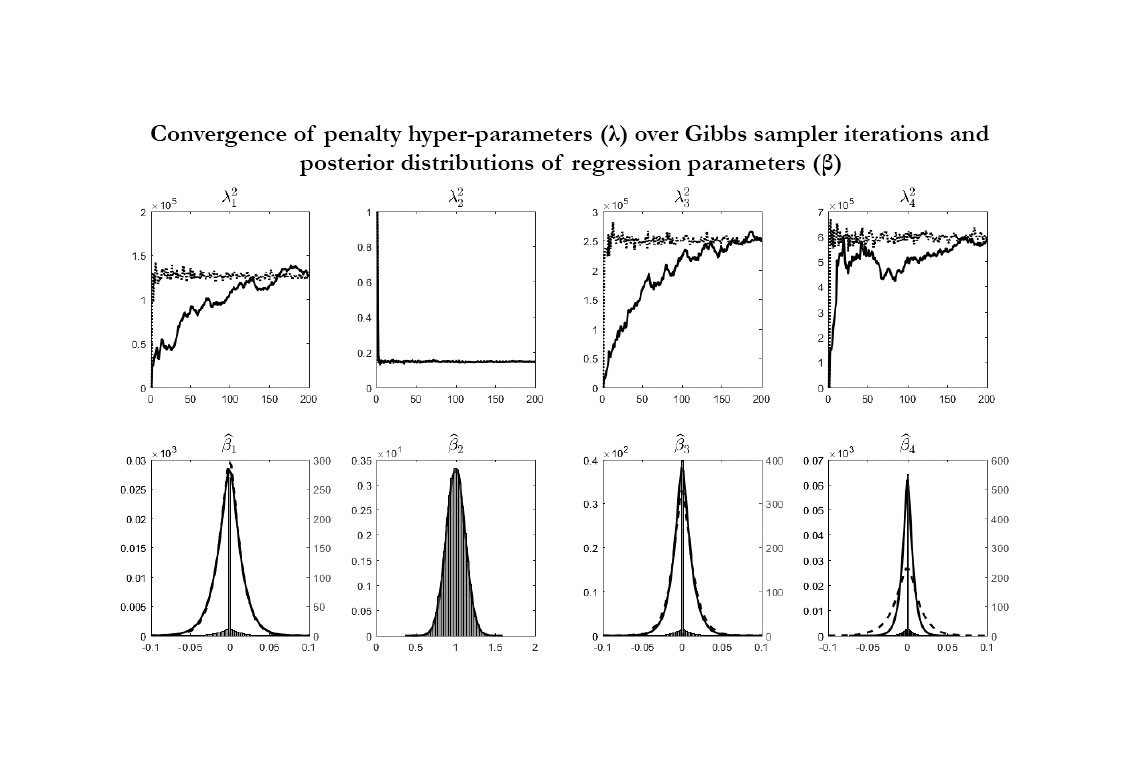
Dans ce document de travail, nous proposons une approche similaire, mais nous nous écartons de la littérature existante sur plusieurs points. Tout d'abord, nous considérons des régressions MIDAS qui s’appuient sur des structures d’agrégation fondées sur les polynômes retard d'Almon, qui ne dépendent que d'un nombre limité de paramètres fonctionnels régissant la forme de la fonction de pondération et qui maintiennent la linéarité dans le modèle de régression. Deuxièmement, nous considérons une pénalité de type Group Lasso, qui s’applique à des groupes distincts de variables explicatives, et nous fixons autant de groupes que le nombre de variables à haute fréquence, ce qui permet à chaque groupe d'inclure le polynôme d'Almon associé à une seule variable. Cette structure est motivée par le fait que si un prédicteur à haute fréquence n'est pas pertinent, il faut s'attendre à ce que des coefficients nuls apparaissent dans tous les paramètres de son polynôme retard. Troisièmement, nous appliquons des techniques bayésiennes pour l'estimation de nos régressions MIDAS pénalisées. Dans le contexte de notre modèle, l'approche bayésienne est particulièrement attractive pour deux raisons. La première est la possibilité d'inclure des à priori de type " spike-and-slab " qui, combinés à la pénalisation du Group Lasso, visent à améliorer la capacité de sélection du modèle. La seconde est l'estimation des hyper-paramètres de pénalisation par une approche automatique et pilotée par les données qui n'a pas recours à des méthodes d’itération extrêmement longues. Dans cet article, nous considérons un algorithme basé sur des approximations stochastiques, qui consiste à approximer les étapes nécessaires pour estimer les hyper-paramètres de telle sorte que des solutions analytiques simples puissent être utilisées. Il s'avère que les hyper-paramètres de pénalisation peuvent être ajustés automatiquement avec un effort de calcul raisonnable comparé aux algorithmes alternatifs existants. Nous montrons par méthodes de simulation (voir figure ci-dessous) que la procédure suggérée fonctionne bien dans notre cadre : les hyper-paramètres de pénalisation (λ) convergent assez rapidement vers leurs valeurs optimales (première ligne), de sorte que les coefficients estimés (β) pour les prédicteurs non pertinents sont correctement centrés à zéro avec une faible variance (deuxième ligne). Plus important encore, les résultats suggèrent des gains de calcul substantiels par rapport à d'autres algorithmes, que nous évaluons d’un facteur de 1 sur 15.

Nous utilisons nos modèles MIDAS dans une application empirique de prévision de la croissance du PIB américain. Nous considérons 42 indicateurs réels et financiers, échantillonnés à des fréquences mensuelles, hebdomadaires et quotidiennes. Nous montrons que nos modèles peuvent fournir des prévisions de court terme supérieures à celles d’une sélection de modèles concurrents. De plus, les résultats suggèrent que les variables financières à haute fréquence peuvent avoir un contenu prédictif, quoique limité, pour la prévision de court terme du PIB.