Working Paper Series no. 861: How do Gasoline Prices Respond to a Cost Shock ?

Price rigidity is a key ingredient in standard macro models to generate short term real effects of monetary policy. A recent theoretical literature has shown that in a very broad class of sticky-price models, the cumulated responses of output to a monetary shock is proportional to the ratio of two moments of the observed price change distribution: the kurtosis of non-zero price changes (i.e. a measure of “fat tails” of the distribution) and the frequency of price changes. This ratio is what we call a sufficient statistic for real effects of a monetary shock. The intuition behind this result is the following: when prices adjust very frequently, prices will respond quickly to the cost shock and the cumulative response of output will be smaller. For a given frequency of price changes, the size of price changes also matters: if firms adjusting their prices are the ones whose prices are the furthest away from the price that would have prevailed under price flexibility, the price response will be quicker and the cumulative real effects smaller. The kurtosis of price changes is shown to capture this “price selection effect” accelerating the price response to a shock. However, empirical evidence testing this sufficient statistic proposition is quite scarce. In this paper, we provide new empirical evidence supporting this prediction, focusing on the cumulated response of prices (CIRP). To do so, we use a dataset covering daily gasoline prices collected in about 10,000 gas stations in France between 2007 and 2018.

Gasoline offers a clean case study for testing the sufficient statistic prediction for at least two reasons: first, we can relate individual prices to observed variations in one of the main component of their costs (i.e. the wholesale gasoline traded on the Rotterdam market) and we are able to derive precise estimates of the price response to a cost shock at the gas station level; second, kurtosis often raises measurement issues because this statistic is quite sensitive to outliers and product heteregoneity. In our dataset, for each gas station, we observe several hundreds of price changes for a homogenous good, which helps us to obtain quite precise measures of kurtosis at the gas station level. We then rely on variation of kurtosis and frequency of price changes across gas stations to test the sufficient statistic prediction.

First, we document that gasoline prices are sticky (relative to the high frequency of shocks): (i) while oil prices vary every day, the typical duration between two gasoline price changes is 4 opening days, (ii) the distribution of gasoline price changes does not mirror the distribution of wholesale price changes: the former displays a two-peak distribution with few small price changes whereas the latter is close to a normal distribution centered around 0; (iii) relating prices to observed cost, we find persistent gaps between actual prices and prices that gas stations would charge if they passed changes in marginal cost into their prices every day; moreover, the probability of changing prices is an increasing function of this gap.

We then estimate the reaction of gasoline prices to a marginal cost shock at both the aggregate and gas station levels. A 1% change in Rotterdam wholesale diesel price translates into a change in retail price of 0.8%, in line with the share of the wholesale gasoline in total costs and a full pass-through of costs to prices. The adjustment is gradual: the pass through takes about 3 weeks. We also find that shocks on the markup (proxied by the average local price changes) are transmitted immediately, with a much smaller pass-through (20%) that gradually fades out to become insignificant after 20 days. We do not find any evidence of asymmetric price reactions to negative or positive shocks.

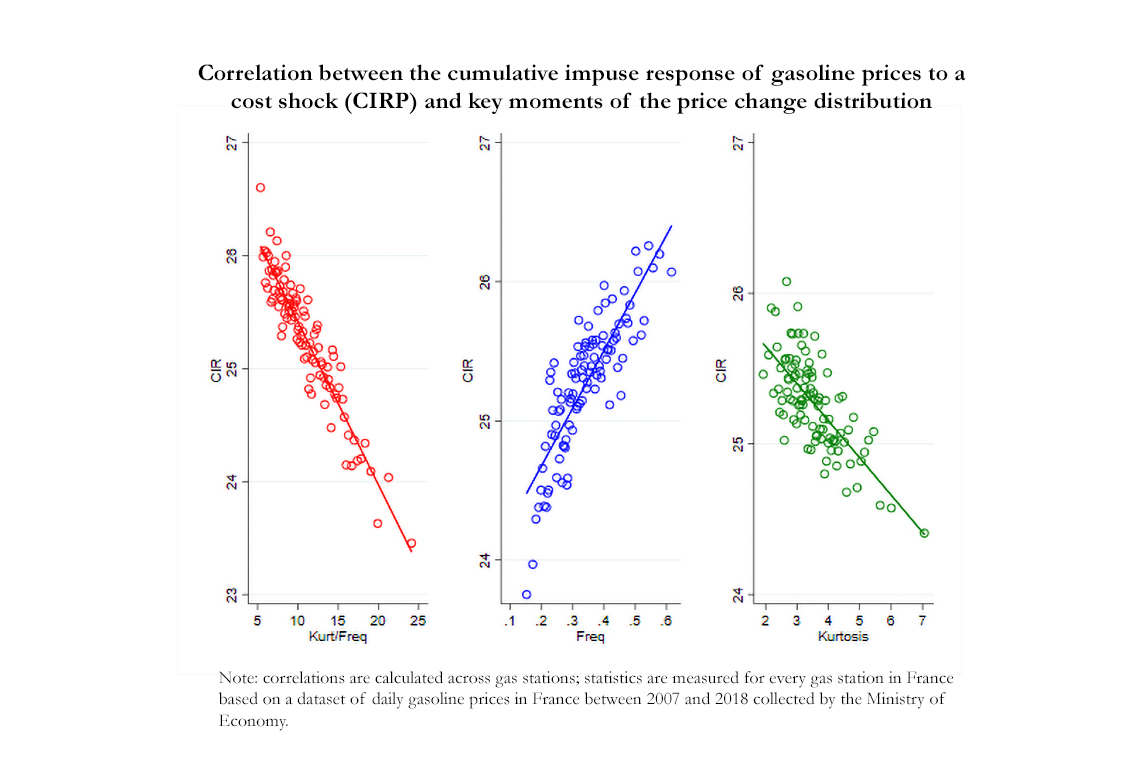
To test the sufficient statistic prediction, we relate the cumulative impulse response function of prices to marginal cost to the ratio of kurtosis over frequency calculated at the gas station level using two different empirical exercises. The first one is conducted pooling all price observations together, while the second exercise uses the cross sectional dispersion of both the cumulated price response and the ratio of the kurtosis to the frequency of price changes at the gas station level. Both empirical exercises provide robust and consistent evidence that this ratio correlates negatively with CIRP as predicted by the sufficient statistic theory (Figure – left panel). The estimated coefficient relating CIRP and the ratio is also close to -0.167, the value predicted by the theory. Besides, both the frequency and the kurtosis of price changes taken separately correlate equally and significantly with CIRP and with the expected sign (Figure center and right panels). Other moments of the price change distribution do not show the same robust and significant relationship with CIRP as the one obtained for the ratio kurtosis over frequency.