Document de travail n°861 : Comment les prix à la pompe réagissent-ils à un choc sur le prix du pétrole ?

Dans les modèles macroéconomiques standard, la rigidité des prix est un ingrédient essentiel pour expliquer les effets réels à court-terme de la politique monétaire. Une littérature théorique récente a montré que, dans une très large classe de modèles à prix rigides, les réponses cumulées de la production à un choc monétaire sont proportionnelles au ratio de deux moments de la distribution des changements de prix observés : la kurtosis des changements (non nuls) de prix (c'est-à-dire une mesure de l’épaisseur des queues de distribution) et la fréquence des changements de prix. On dit que ce ratio représente une statistique suffisante pour quantifier les effets réels d'un choc monétaire. L'intuition derrière ce résultat est la suivante : lorsque les prix s'ajustent très fréquemment, les prix répondent rapidement au choc de coût et la réponse cumulée de la production est plus faible. Pour une fréquence donnée des changements de prix, la taille des changements de prix importe également : si les entreprises qui ajustent leurs prix sont celles dont les prix sont les plus éloignés du prix qui aurait prévalu sans rigidité, la réponse des prix sera plus rapide et les effets réels cumulés plus faibles. Il est démontré que la kurtosis des variations de prix capture cet "effet de sélection" accélérant la réponse des prix à un choc. Cependant, il existe peu de résultats empiriques testant cette prédiction de statistique suffisante. C’est ce que nous faisons dans cet article en étudiant la réponse cumulée des prix (CIRP). Pour ce faire, nous utilisons un ensemble de données couvrant les prix quotidiens de l'essence collectés dans environ 10 000 stations-service en France entre 2007 et 2018.

Le cas des prix à la pompe est un cadre bien adapté pour tester cette prédiction pour au moins deux raisons : premièrement, la composante principale du coût est le prix de gros négocié sur le marché de Rotterdam et nous pouvons estimer précisément au niveau de la station-service la réponse des prix à un choc de coût; deuxièmement, la kurtosis soulève souvent des problèmes de mesure car cette statistique est assez sensible aux valeurs aberrantes et à l'hétérogénéité des produits. Dans notre base de données, pour chaque station-service, nous observons plusieurs centaines de changements de prix pour un bien homogène, ce qui nous permet d'obtenir des mesures assez précises de la kurtosis au niveau de la station-service. Les variations de la kurtosis et de la fréquence des changements de prix entre les stations-service permettent de tester si la statistique est suffisante.

Premièrement, nous démontrons que les prix de l'essence sont rigides (par rapport à la fréquence élevée des chocs) : (i) alors que les prix du pétrole varient chaque jour, la durée typique entre deux changements de prix de l'essence est de 4 jours ouvrés, (ii) la distribution des changements de prix de l'essence ne reflète pas la distribution des changements du prix de gros : la première est représentée par une distribution à deux pics avec peu de petits changements de prix alors que la seconde est proche d'une distribution normale centrée autour de 0 ; (iii) en reliant les prix au coût observé, nous trouvons des écarts persistants entre les prix pratiqués et les prix que les stations-service appliqueraient si elles ajustaient chaque jour les prix en fonction du coût marginal ; de plus, la probabilité de changer les prix est une fonction croissante de cet écart entre le prix appliqué et le prix qui prévaudrait sans rigidité.

Nous estimons ensuite la réaction des prix à la pompe à un choc sur le coût marginal à la fois au niveau global et au niveau des stations-service. Une variation de 1 % du prix de gros du gazole à Rotterdam se traduit par une variation du prix de détail de 0,8 %, ce qui correspond à la part du gazole raffiné dans les coûts totaux et à une répercussion complète des coûts sur les prix. L'ajustement est progressif : la répercussion prend environ 3 semaines. Nous constatons également que les chocs sur les marges (approximées par les changements de prix des stations voisines) sont transmis immédiatement, avec une transmission beaucoup plus faible (20 %) qui s'estompe progressivement pour devenir non significative après 20 jours. Nous ne trouvons aucune preuve d’une réaction asymétrique des prix à un choc positif ou négatif.

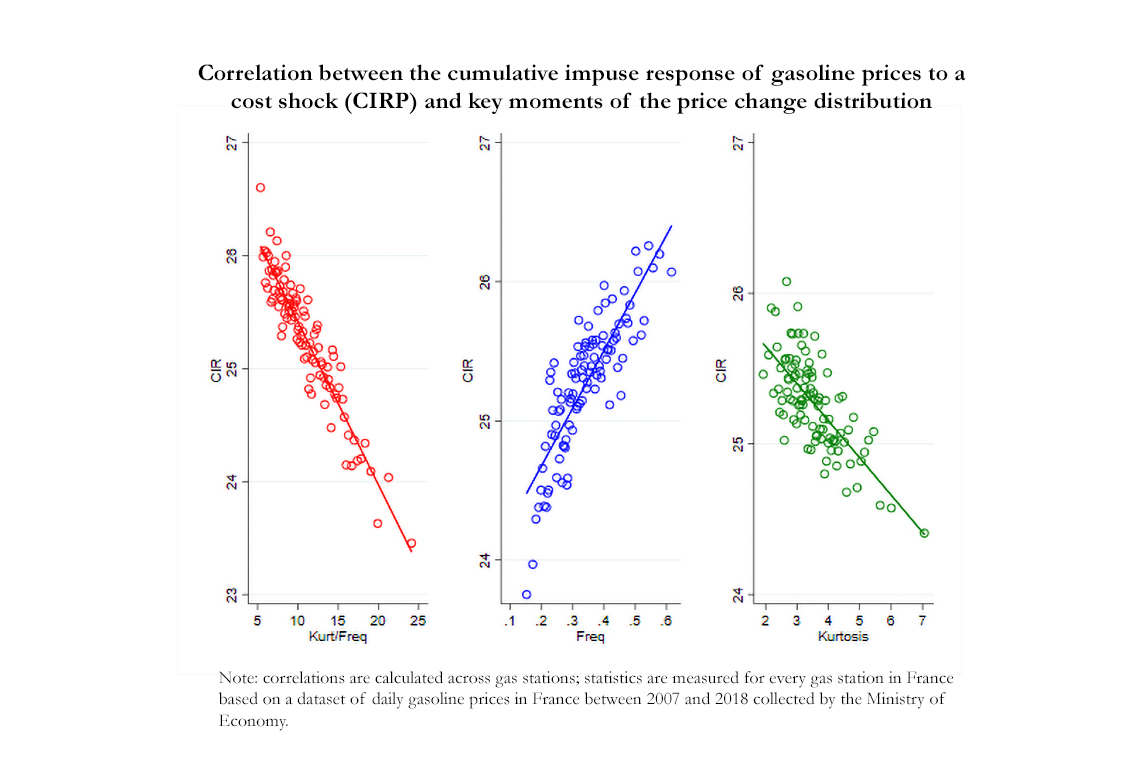
Pour tester la prédiction de la statistique suffisante, nous mesurons la corrélation entre la fonction de réponse cumulée des prix au coût marginal et le ratio kurtosis sur fréquence calculé au niveau de la station-service sur la base de deux exercices empiriques différents. Le premier est réalisé au niveau agrégé, tandis que le second est une estimation de la réponse cumulée des prix par rapport au ratio kurtosis sur fréquence au niveau de chaque station. Les deux exercices empiriques fournissent des preuves solides et cohérentes que le CIRP et ce ratio sont négativement corrélés, en accord avec la prédiction (figure - panneau de gauche). Le coefficient de régression estimé reliant le CIRP et le ratio est également proche de -0,167, la valeur prédite par la théorie. En outre, la fréquence et la kurtosis, pris séparément, sont corrélés de manière égale et significative avec le CIRP et avec le signe attendu (figure - panneaux central et droit). Les autres moments de la distribution ne sont pas aussi fortement corrélés avec le CIRP que la fréquence et la kurtosis.