Document de travail n°670 : Cible d'inflation optimale et taux d'intérêt naturel
Philippe Andrade, Jordi Galí, Hervé Le Bihan & Julien Matheron étudient comment les variations du taux d'intérêt réel d’état-stationnaire influent sur la cible d'inflation optimale. Ils utilisent pour cela un modèle DSGE de type New Keynésien estimé pour les États-Unis et la zone euro dans lequel ils intègrent une borne inférieure (à zéro ou effective) sur le taux d'intérêt nominal. Ils obtiennent que la relation entre taux d'inflation optimal et taux d'intérêt réel d’état-stationnaire est décroissante mais que sa pente n'est pas nécessairement un pour un : les hausses du taux d'inflation optimal sont généralement inférieures aux baisses du taux d'intérêt réel d’état-stationnaire. Leur approche leur permet d'évaluer la cible d'inflation optimale qui tient compte de l'incertitude relative aux paramètres auxquels est confronté le décideur, en particulier l'incertitude relative aux déterminants du taux d'intérêt réel d’état-stationnaire. Si l’on se situe dans la plage de valeurs du taux d’intérêt réel qui correspond à celles observées aux États-Unis et dans la zone euro avant la crise, la pente de la courbe est proche de -0,9. Cette conclusion reste valide lorsqu’on prend en compte l'incertitude des paramètres du modèle.
L'objectif d'inflation que les banques centrales s'engagent à atteindre est une dimension clé de la stratégie moderne de politique monétaire. Parmi les raisons d'avoir une inflation strictement positive figurent les coûts induits par la borne à zéro (ZLB) sur les taux d'intérêt. La ZLB entrave la capacité de la politique monétaire à stabiliser l'économie, entraînant des épisodes plus fréquents (et potentiellement prolongés) de récessions et une inflation inférieure à la cible. Une cible d'inflation positive peut être bénéfique, car elle augmente le niveau d'équilibre des taux d'intérêt nominaux et limite donc la probabilité d'épisodes de ZLB.
Des recherches récentes, souvent associées à la notion de "stagnation séculaire", soulignent que les taux d'intérêt réels peuvent avoir structurellement baissé au cours de la dernière décennie. Ce n’est pas neutre pour la politique monétaire : pour une inflation moyenne donnée, un taux réel en régime permanent plus faible implique que le taux d'intérêt nominal atteindra plus fréquemment la ZLB. Face à ce risque, et pour le contrer, plusieurs économistes éminents ont plaidé avec force en faveur d'un relèvement de la cible d'inflation. Bien que la proposition soit relativement intuitive, la réponse à la question pratique de savoir dans quelle mesure l'objectif d’inflation devrait être relevé n'est pas évidente. En effet, les avantages de limiter la probabilité de ZLB, qui est un événement peu fréquent, doivent être comparés aux coûts de distorsion plus élevés qu'entraîne une augmentation permanente de la cible d'inflation.
Le présent document aborde cette question en évaluant de quelle façon l'arbitrage entre le coût de l'inflation et le coût de la ZLB est affecté par une telle baisse structurelle potentielle du taux d'intérêt réel. Plus précisément, nous utilisons un modèle macroéconomique structurel, estimé empiriquement, pour caractériser la relation entre la cible d'inflation optimale (π*) et le taux d'intérêt réel en régime permanent (r*) et dans quelle mesure la source des variations du taux d'intérêt réel de régime permanent affecte cette relation.
Nos résultats sont obtenus à partir de simulations systématiques d'un modèle DSGE « nouveau keynésien » estimé sur les États-Unis et la zone euro. Le cadre se caractérise par : (i) la rigidité des prix et l'indexation imparfaite des prix sur l'inflation tendancielle non nulle, (ii) la rigidité des salaires et l'indexation imparfaite des salaires sur l'inflation et le progrès technique, et (iii) une contrainte ZLB sur le taux d'intérêt nominal. Les deux premières caractéristiques impliquent la présence de coûts potentiellement substantiels associés à une inflation non nulle des salaires ou des prix. La troisième caractéristique justifie un taux d'inflation strictement positif, afin d'atténuer l'incidence et les effets négatifs de la ZLB. À notre connaissance, ces trois caractéristiques n'ont pas été prises en compte conjointement dans les analyses précédentes de l'inflation optimale.
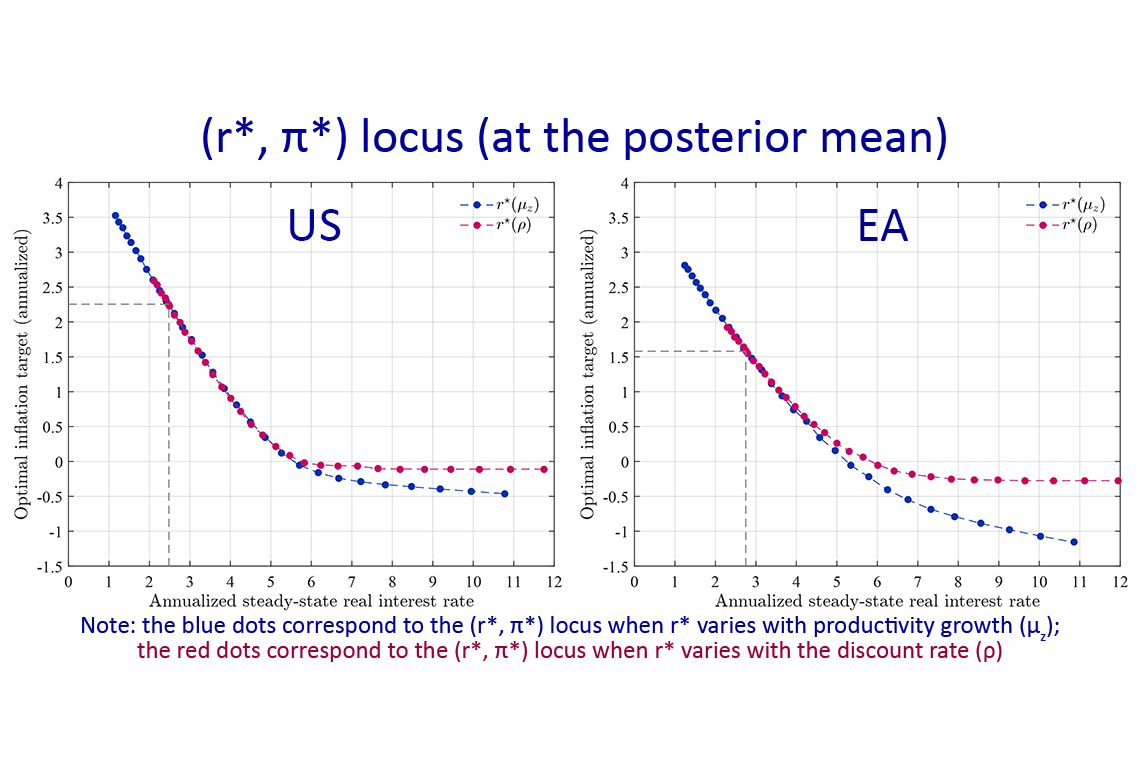
La figure ci-dessus illustre nos principaux résultats qui peuvent être résumés comme suit : (i) La relation entre r*et π* est décroissante, mais sa pente n’est pas nécessairement égale à -1 ; (ii) dans le voisinage des valeurs d'avant crise de r*, la pente de la relation (r*, π*) est proche de -0.9 ; c'est-à-dire qu’une baisse de 100 points de base du taux d'intérêt réel en régime permanent justifie une augmentation de 90 points de base de la cible d'inflation ; et (iii) pour une fourchette plausible de valeurs de r*, la relation est largement robuste à la source sous-jacente de variation de r*.
Comme nous effectuons une estimation bayésienne complète du modèle sur les données américaines et de la zone euro, nous pouvons en déduire une cible d'inflation optimale tenant compte de l'incertitude sur les paramètres à laquelle est confronté le décideur politique. Lorsque cette incertitude - y compris celle relative aux déterminants du taux d'intérêt réel en régime permanent - est prise en compte, les valeurs de la cible optimale d'inflation sont plus élevées : 2,40 % au lieu de 2 % pour les États-Unis et 2,20 % au lieu de 1,5 % pour la zone euro. Toutefois, les simulations montrent que la cible optimale d'inflation augmente encore d'environ 90 points de base en réponse à une baisse de l'ensemble de la distribution de r* de 100 points de base.
Ce résultat principal est robuste à plusieurs hypothèses alternatives décrites dans le document.
Télécharger la version PDF du document

- Publié le 26/03/2018
- 62 page(s)
- EN
- PDF (2.57 Mo)
Mis à jour le : 26/03/2018 16:01